(問1)I 1 と置きます。そうしますと、オームの法則 より、
I 1 = \(\large{\frac{E}{R}}\)
フレミングの左手の法則 を適用しますと力の向きは 右向き で、
電流が磁場から受ける力 の大きさ(F = IBl sinθ )を F 1 と置きますと、
F 1 = I 1 Bd = \(\large{\frac{EBd}{R}}\)
(問2)V = vBl V 2 と置きますと、
V 2 = vBd
であり、その向き は紙面こちら向きです。
I 2 と置いて左図のような左回りのループの電位を考えますと、
ア→イ では電池によって電圧が上げられ + E 、ウ→エ では電流が紙面向こう向きに流れ抵抗によって電位が降下し - RI 2 、*
これは間違いやすいです。『キルヒホッフの法則』項の『経路その1 』の説明をよくお読みください。
閉じる vBd となります。
よって、キルヒホッフの第2法則 の式は
+ E - RI 2 - vBd = 0
∴ RI 2 = E - vBd
∴ I 2 = \(\large{\frac{E-vBd}{R}}\)
スイッチを入れた直後の問1の電流に比べて小さくなってます。v で走り出すと誘導起電力が発生し、邪魔され、電流が小さくなります。
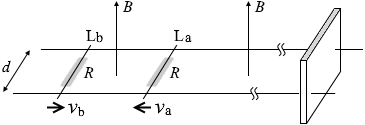
(問3)a が動かされ、それによって電磁誘導が起こり、誘導起電力 が発生し、電流が流れ、棒Lb にも流れ、磁場の中の電流は力を受ける ので棒Lb も動いた、ということです。(このとき棒Lb にも電磁誘導が起こります。棒La と棒Lb は電池のような 役目をします。)
細かく見ていきますと、
a は右に動かされ(このときの速さは v 0 )、電磁誘導が起こり、
I 3 と置きます)、
フレミングの左手の法則 により左向きであり、棒La は減速します。このときの速さが v a ということです。
a に流れた電流 I 3 は棒Lb にも流れ、
v b ということです。
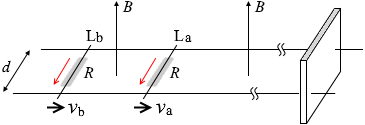
b は上向きの磁場が減るように動きますから、レンツの法則により上向きの磁場を増やすような向きです。紙面こちら向きです。電流は紙面向こう向きですから、電流を邪魔するような向きに誘導起電力が発生するということです。*
棒La の誘導起電力のみによって発生した電流を I 3 と置くようなことを上で書きましたが、b の誘導起電力による妨害も含めた電流の大きさが I 3 です。
閉じる
カ→キ では、a が v a で動くことによって誘導起電力が発生し + v a Bd
I 3 の電流が紙面こちら向きに流れるので抵抗によって電位が降下し - RI 3 、
ク→ケ では、b が v b で動くことによって紙面こちら向きに誘導起電力が発生し - v b Bd 、
I 3 の電流が紙面向こう向きに流れるので抵抗によって電位が降下し - RI 3 。
よって、キルヒホッフの第2法則 の式は
+ v a Bd - RI 3 - v b Bd - RI 3 = 0
+ v a Bd - v b Bd - 2RI 3 = 0
∴ 2RI 3 = v a Bd - v b Bd
∴ I 3 = \(\large{\frac{(v_a-v_b)Bd}{2R}}\)
電流の大きさがわかったので磁場から受ける力の大きさ (F = IBl sinθ )が求められ、
棒La にはたらく力を F a としますと、
F a = I 3 Bd = \(\large{\frac{(v_a-v_b)B^2d^2}{2R}}\)
向きは(上で説明したように) 左向き
棒Lb にはたらく力を F b としますと、
F b = I 3 Bd = \(\large{\frac{(v_a-v_b)B^2d^2}{2R}}\)
向きは(上で説明したように) 右向き
力の大きさは同じで向きが逆です。棒La も棒Lb も右に進んで行きますが、棒La は減速し、棒Lb は加速していきます。
(問4)内力のみがはたらくときは、運動量保存の法則が成り立つ のです。問3で調べたように2つの棒にはたらく力は向きが逆で大きさが同じです。これは内力とみなせます。外力がはたらいておらず内力のみがはたらいているときは運動量が保存します。
等しくなったときの速度を v 3 と置きますと、
(初速を与えた瞬間)
棒La の運動量:mv 0
棒Lb の運動量:m ⋅0
(等しくなった瞬間)
棒La の運動量:mv 3
棒La の運動量:mv 3
運動量保存の法則より、mv 0 + m ⋅0 = mv 3 + mv 3
∴ v 0 = 2v 3
∴ v 3 = \(\large{\frac{1}{2}}\)v 0
次に運動エネルギーについて考えてみますと、
(初速を与えた瞬間)
棒La の運動エネルギー:\(\large{\frac{1}{2}}\)mv 0 2
棒Lb の運動エネルギー:\(\large{\frac{1}{2}}\)m ⋅02
(等しくなった瞬間)
棒La の運動エネルギー:\(\large{\frac{1}{2}}\)mv 3 2 (=\(\large{\frac{1}{2}}\)m \(\large{\frac{1}{4}}\)v 0 2 )
棒La の運動エネルギー:\(\large{\frac{1}{2}}\)mv 3 2 (=\(\large{\frac{1}{2}}\)m \(\large{\frac{1}{4}}\)v 0 2 )
(初速を与えた瞬間)と(等しくなった瞬間)の運動エネルギーを比較してみますと、
\((\)\(\large{\frac{1}{2}}\)mv 0 2 + \(\large{\frac{1}{2}}\)m ⋅02 \()\) - \((\)\(\large{\frac{1}{2}}\)m \(\large{\frac{1}{4}}\)v 0 2 + \(\large{\frac{1}{2}}\)m \(\large{\frac{1}{4}}\)v 0 2 \()\)
= \(\large{\frac{1}{2}}\)mv 0 2 - m \(\large{\frac{1}{4}}\)v 0 2
= \(\large{\frac{1}{4}}\)mv 0 2
これだけの運動エネルギーが減っているわけですが、これがまさに回路で消費されたエネルギーです。回路が発熱したわけです。ジュール熱 です。
答え \(\large{\frac{1}{4}}\)mv 0 2
この話は『運動量保存と力学的エネルギー』項の『片方が静止していて、e=0 』に似ています。あと、『渦電流 』にも似ています。
(問5)
*
磁場の中を動く導体棒は電池 』や磁場にすっぽり覆われた中で角度を変えずに動かしても誘導起電力は発生しない 』で閉じる
電流が流れないので棒は力を受けません(F = IBd の I が 0 )。力を受けないので2本の棒は等速直線運動をします 。問4の状態以降、棒は等速直線運動をするのです。
a と板との衝突は弾性衝突 ですから、向きを変えてからも速度の大きさは変わりません。
2つの棒は質量が同じですから受ける力が同じなら加速度も同じ です。つまり、
答え 棒La と棒Lb は向かい合う方向に同じ大きさの加速度で減速していき、同時に静止する。
エネルギーに着目しますと、問3で \(\large{\frac{1}{2}}\)mv 0 2 のエネルギーが与えられ、問4で \(\large{\frac{1}{4}}\)mv 0 2 のエネルギーが消費され、問5で残りの \(\large{\frac{1}{4}}\)mv 0 2 が消費されるということになります。
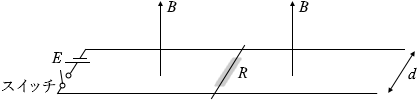
 まず、回路に流れる電流の大きさを求めます。I1 と置きます。そうしますと、
まず、回路に流れる電流の大きさを求めます。I1 と置きます。そうしますと、 電池の向きからしますとこの電流は紙面向こう向きであり、
電池の向きからしますとこの電流は紙面向こう向きであり、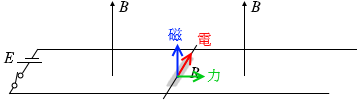
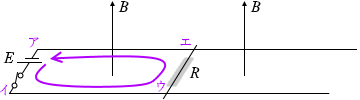 求める電流を I2 と置いて左図のような左回りのループの電位を考えますと、
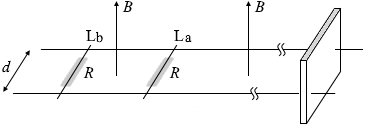
求める電流を I2 と置いて左図のような左回りのループの電位を考えますと、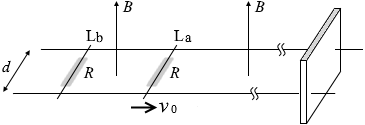 始め、棒Laは右に動かされ(このときの速さは v0)、電磁誘導が起こり、
始め、棒Laは右に動かされ(このときの速さは v0)、電磁誘導が起こり、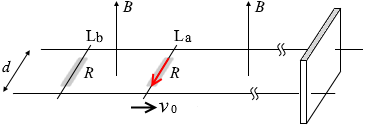 上向きの磁場が増えるから、レンツの法則により下向きの磁場を増やすような向きに誘導起電力が発生し、電流が流れ(このときの電流の大きさを I3 と置きます)、
上向きの磁場が増えるから、レンツの法則により下向きの磁場を増やすような向きに誘導起電力が発生し、電流が流れ(このときの電流の大きさを I3 と置きます)、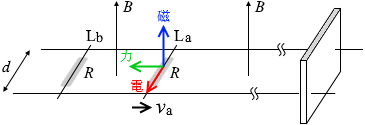 磁場の中の電流は電磁力を受けますが、その向きは
磁場の中の電流は電磁力を受けますが、その向きは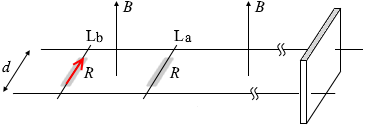 棒Laに流れた電流 I3 は棒Lbにも流れ、
棒Laに流れた電流 I3 は棒Lbにも流れ、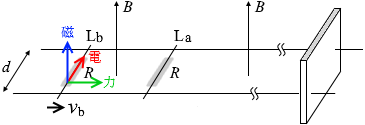 フレミングの左手の法則により右向きに力を受け動き出します。このときの速さが vb ということです。
フレミングの左手の法則により右向きに力を受け動き出します。このときの速さが vb ということです。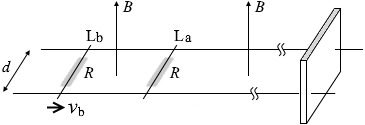 磁場の中で導線が動くので電磁誘導が起こり誘導起電力が発生しますが、
磁場の中で導線が動くので電磁誘導が起こり誘導起電力が発生しますが、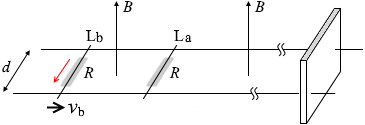 その向きは、棒Lbは上向きの磁場が減るように動きますから、レンツの法則により上向きの磁場を増やすような向きです。紙面こちら向きです。電流は紙面向こう向きですから、電流を邪魔するような向きに誘導起電力が発生するということです。
その向きは、棒Lbは上向きの磁場が減るように動きますから、レンツの法則により上向きの磁場を増やすような向きです。紙面こちら向きです。電流は紙面向こう向きですから、電流を邪魔するような向きに誘導起電力が発生するということです。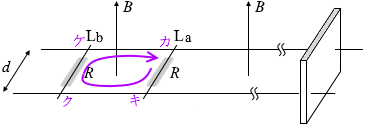 ここで、左図のような右回りのループの電位を考えてみますと、
ここで、左図のような右回りのループの電位を考えてみますと、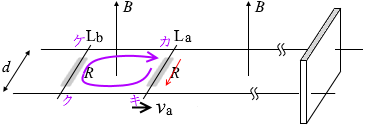
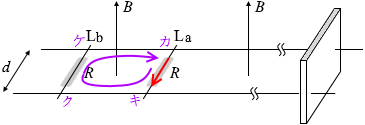 I3 の電流が紙面こちら向きに流れるので抵抗によって電位が降下し - RI3 、
I3 の電流が紙面こちら向きに流れるので抵抗によって電位が降下し - RI3 、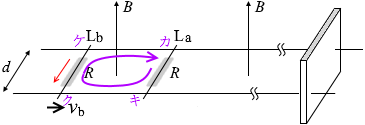
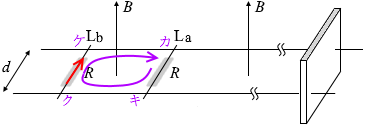 I3 の電流が紙面向こう向きに流れるので抵抗によって電位が降下し - RI3 。
I3 の電流が紙面向こう向きに流れるので抵抗によって電位が降下し - RI3 。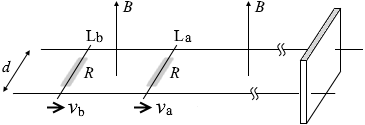 2本の棒の速度が同じになる問4のような状態になると、電流が流れなくなります。
2本の棒の速度が同じになる問4のような状態になると、電流が流れなくなります。
 誘導起電力の大きさが同じになって打ち消し合うからです。
誘導起電力の大きさが同じになって打ち消し合うからです。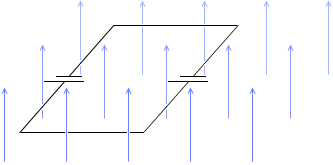 『
『 『
『 そして、棒Laと板との衝突は
そして、棒Laと板との衝突は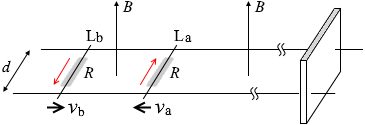 そして、向きが変わったので今度は誘導起電力が打ち消し合わず電流が発生します。
そして、向きが変わったので今度は誘導起電力が打ち消し合わず電流が発生します。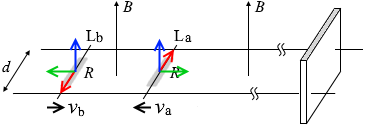 電流の大きさは同じなので受ける力の大きさも同じです。
電流の大きさは同じなので受ける力の大きさも同じです。