(問1)
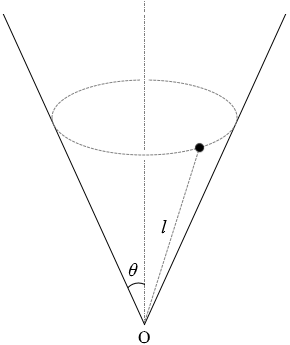
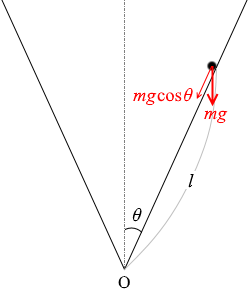 小物体に掛かる重力は mg で、運動方向の成分は mgcosθ であり、運動方向の加速度を α と置いて運動方程式を立てますと、
小物体に掛かる重力は mg で、運動方向の成分は mgcosθ であり、運動方向の加速度を α と置いて運動方程式を立てますと、
mα = mgcosθ
∴ α = gcosθ
となりますが、g の値は一定であるので gcosθ も一定であるわけです。そうしますとこの運動は等加速度直線運動(あるいは鉛直投射運動において g を gcosθ としたもの)と考えることができます。
求める時間を t と置いて、等加速度直線運動(あるいは鉛直投射)の変位の式(x = v0t + \(\large{\frac{1}{2}}\)at2)を立てますと、
l = 0×t + \(\large{\frac{1}{2}}\)(gcosθ)t2
∴ l = \(\large{\frac{1}{2}}\)(gcosθ)t2
∴ t2 = \(\large{\frac{2l}{g\cosθ}}\)
∴ t = \(\sqrt{\large{\frac{2l}{g\cosθ}}}\)
(問2)
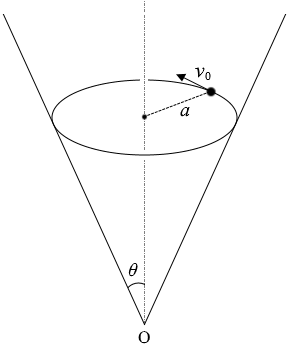
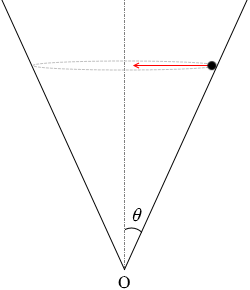 等速円運動をしているということは向心力がはたらいているということであり、半径 a の円を描いているということは向心力の大きさは
等速円運動をしているということは向心力がはたらいているということであり、半径 a の円を描いているということは向心力の大きさは
m\(\large{\frac{{v_0}^2}{a}}\)
であるはずです。(『円錐振り子』参照)
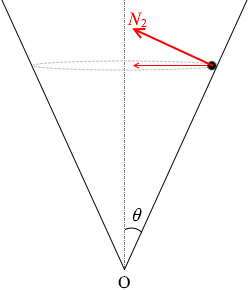 この向心力は垂直抗力(N2 とする)の水平成分 N2cosθ であり、
この向心力は垂直抗力(N2 とする)の水平成分 N2cosθ であり、
m\(\large{\frac{{v_0}^2}{a}}\) = N2cosθ ……①
が成り立ちます。(円運動の運動方程式です)
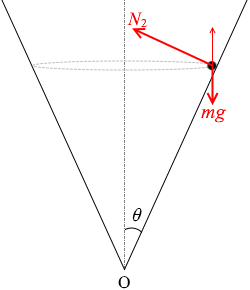 また、小物体は鉛直方向には動かないので、垂直抗力の鉛直成分(N2sinθ)と重力 mg はつり合っているはずです。
また、小物体は鉛直方向には動かないので、垂直抗力の鉛直成分(N2sinθ)と重力 mg はつり合っているはずです。
N2sinθ = mg
∴ N2 = \(\large{\frac{mg}{\sinθ}}\)
この式を①式に代入して、
m\(\large{\frac{{v_0}^2}{a}}\) = \(\large{\frac{mg}{\sinθ}}\)cosθ
∴ \(\large{\frac{{v_0}^2}{a}}\) = \(\large{\frac{g\cosθ}{\sinθ}}\) (これは加速度のことです
等速円運動の加速度は
\(\Big(\)\(\large{\frac{v^2}{r}}\)\(\Big)\) = \(\large{\frac{{v_0}^2}{a}}\)
であり、これが
\(\large{\frac{g\cosθ}{\sinθ}}\) = \(\large{\frac{g}{\tanθ}}\)
であるということです。
加速度は θ のみで決まります。
)
∴ \(\large{\frac{a}{{v_0}^2}}\) = \(\large{\frac{\sinθ}{g\cosθ}}\)
∴ a = \(\large{\frac{{v_0}^2\tanθ}{g}}\) ……②
(余談:1)
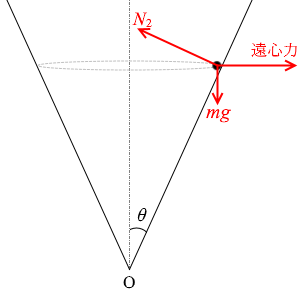 垂直抗力 N2 と 重力 mg と遠心力 m\(\large{\frac{{v_0}^2}{a}}\) がつり合っていると考えることもできます。
垂直抗力 N2 と 重力 mg と遠心力 m\(\large{\frac{{v_0}^2}{a}}\) がつり合っていると考えることもできます。
垂直抗力 = \(\large{\frac{1}{\sinθ}}\)×重力
遠心力 = \(\large{\frac{1}{\tanθ}}\)×重力
の関係があります。垂直抗力も遠心力も θ のみで決まります。高さは無関係です。
(余談:3)
半径 a 、初速度 v0 、角度 θ が a = \(\large{\frac{{v_0}^2\tanθ}{g}}\) というバランスを取ったときに小物体は等速円運動をします。ちょっとでも v0 が大きかったりすると、小物体は上昇してしまいます。上昇していくと a が大きくなってバランスが取れ、その高さで等速円運動します。v0 が小さければ小物体は下降していき、ある高さでバランスが取れて等速円運動をします。初速を与えるときのエネルギーの大きさで小物体が等速円運動する高さが決まります。
(問3)
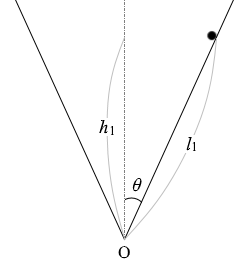
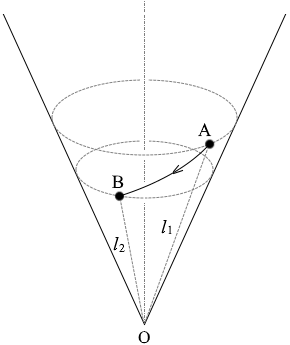
求める速さを v2 、点Aの高さを h1 、点Bの高さを h2 とします。
点Aでの小物体の力学的エネルギーは
運動エネルギー:\(\large{\frac{1}{2}}\)mv12
位置エネルギー: mgh1
\(\large{\frac{1}{2}}\)mv12 + mgh1
点Bでの小物体の力学的エネルギーは
運動エネルギー:\(\large{\frac{1}{2}}\)mv22
位置エネルギー:mgh2
\(\large{\frac{1}{2}}\)mv22 + mgh2
力学的エネルギー保存の法則より、上の2式は等しいから、
\(\large{\frac{1}{2}}\)mv12 + mgh1 = \(\large{\frac{1}{2}}\)mv22 + mgh2 ……③
∴ v12 + 2gh1 = v22 + 2gh2
∴ v22 = v12 + 2gh1 - 2gh2
∴ v22 = v12 + 2g(h1 - h2)
∴ v2 = \(\sqrt{{v_1}^2+2g(h_1-h_2)}\) ……④
∴ v2 = \(\sqrt{{v_1}^2+2g(l_1-l_2)\cosθ}\) (∵ h1 = l1cosθ , h2 = l2cosθ
 )
)
(余談:5)
問2で求めた②式
a = \(\large{\frac{{v_0}^2\tanθ}{g}}\)
を変形しますと、
\(\large{\frac{a}{\tanθ}}\) = \(\large{\frac{{v_0}^2}{g}}\)
であり、v0 で等速円運動しているときの高さを h0 と置きますと、\(\large{\frac{a}{\tanθ}}\) = h0
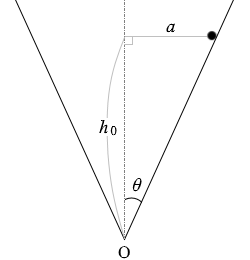 であるので、
であるので、
h0 = \(\large{\frac{{v_0}^2}{g}}\) ……⑤
となります。
これはつまり、等速円運動の(周回の)速さは高さのみで決まるということであり、質量や半径や θ には無関係ということです。
また、このときの力学的エネルギーを求めてみますと、
\(\large{\frac{1}{2}}\)mv02 + mgh0 = \(\large{\frac{1}{2}}\)mgh0 + mgh0 (∵ ⑤式)
= \(\large{\frac{3}{2}}\)mgh0
これは、h0 の高さ、v0 の速さで等速円運動をしている物体の力学的エネルギーは、その \(\large{\frac{3}{2}}\) の高さに置かれた場合の物体の力学的エネルギーと同じ、といえるということです。
③式のような力学的エネルギー保存の法則の式を書けば、
\(\large{\frac{1}{2}}\)mv02 + mgh0 = \(\large{\frac{1}{2}}\)m⋅02 + \(\large{\frac{3}{2}}\)mgh0
となります。
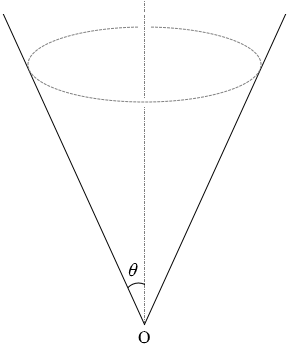
逆さ円錐面内側の任意の位置で静かに放した球は
蛇行しながら徐々に安定状態(等速円運動)になります。
、その\(\large{\frac{2}{3}}\)の高さの位置で等速円運動をするということです。円錐面での運動の面白い特徴です。
 小物体に掛かる重力は mg で、
小物体に掛かる重力は mg で、 等速円運動をしているということは
等速円運動をしているということは この向心力は垂直抗力(N2 とする)の水平成分 N2cosθ であり、
この向心力は垂直抗力(N2 とする)の水平成分 N2cosθ であり、 また、小物体は鉛直方向には動かないので、垂直抗力の鉛直成分(N2sinθ)と重力 mg はつり合っているはずです。
また、小物体は鉛直方向には動かないので、垂直抗力の鉛直成分(N2sinθ)と重力 mg はつり合っているはずです。 垂直抗力 N2 と 重力 mg と遠心力 m\(\large{\frac{{v_0}^2}{a}}\) がつり合っていると
垂直抗力 N2 と 重力 mg と遠心力 m\(\large{\frac{{v_0}^2}{a}}\) がつり合っていると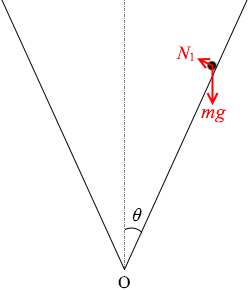 問1においても垂直抗力は存在します。斜面方向の運動と無関係なので無視しただけです。大きさは mgsinθ です。N1 < N2 です
問1においても垂直抗力は存在します。斜面方向の運動と無関係なので無視しただけです。大きさは mgsinθ です。N1 < N2 です
