高校物理で使う公式を列挙してみました。しかし丸暗記しようとするのはおやめください。物理の問題は公式を覚えておけば解けるというものではありません。本稿は試験前の総チェック、頭の整理、気休めとしてご利用ください。
力学
力の合成・分解
力は平行四辺形の法則によって合成したり分解したりすることができます。物体の運動を考える際は『運動方向』と『運動方向と垂直な方向』に分解することが多いです。
力のつり合い
力がつり合っているとき、物体のスピードは 0 か等速です。逆に、0 か等速のとき、力はつり合っています。
作用・反作用の法則
押すと同じ力で押し返され、引くと同じ力で引き返されます。
張力
ピンと張ったロープには、どこもかしこも同じ大きさの力がはたらいています。
\(\boldsymbol{F = μN}\)
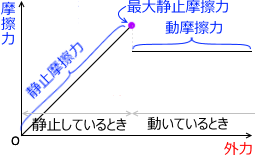 静止摩擦力は変化し、最大静止摩擦力は変化せず、動摩擦力も変化しません。
静止摩擦力は変化し、最大静止摩擦力は変化せず、動摩擦力も変化しません。
摩擦角 \(\boldsymbol{θ}\)
\(\boldsymbol{μ = \tanθ}\)
\(\boldsymbol{P= \large\frac{F}{S}}\)
水圧
水圧の大きさは深さのみによります。
浮き沈みに関しては浮力だけでは決まらないことに注意してください。
\(\boldsymbol{M = Fl = Fr\sinθ}\)
作用線の定理
剛体の力のつり合いを考えるとき、力をその作用線上で移動させてもその効果は変わりません。
\(\boldsymbol{\vec{F}_1 + \vec{F}_2 + \vec{F}_3 + … = 0}\)
\(\boldsymbol{M_1 + M_2 + M_3 + … = 0}\)
特に2番目の式を使って問題を解くことが多いです。そのとき、回転の中心を計算がしやすい位置に自分で勝手に設定します。
\(\boldsymbol{M = Fl}\)
\(\boldsymbol{x_{\small{\rm G}} = \large\frac{m_1x_1\ +\ m_2x_2}{m_1\ +\ m_2}}\)
\(\boldsymbol{x_{\small{\rm G}} = \large\frac{m_1x_1\ +\ m_2x_2\ +\ \ \cdots\ +\ m_nx_n}{m_1\ +\ m_2\ +\ \ \cdots\ +\ m_n}}\)
\(\boldsymbol{y{\small{\rm G}} = \large\frac{m_1y_1\ +\ m_2y_2\ +\ \ \cdots\ +\ m_ny_n}{m_1\ +\ m_2\ +\ \ \cdots\ +\ m_n}}\)
相対速度
「Aに対するBの相対速度」といったら「Aを基準としたBの相対速度」です。相対速度は (対象物)-(基準) です。平面上の相対速度であればベクトルの減法を使います。
\(\boldsymbol{v = v_0 + at}\)
\(\boldsymbol{x = v_0t + {\large\frac{1}{2}}at^2}\)
\(\boldsymbol{v^2 - {v_0}^2 = 2ax}\)
速度 \(\boldsymbol{v = gt}\)
変位 \(\boldsymbol{y = {\large\frac{1}{2}}gt^2}\)
\(t\) を含まない式 \(\boldsymbol{v^2 = 2gy}\)
鉛直下方投射 (鉛直下向きが正)
速度 \(\boldsymbol{v = v_0 + gt}\)
変位 \(\boldsymbol{y = v_0t + {\large{\frac{1}{2}}}gt^2}\)
\(t\) を含まない式 \(\boldsymbol{v^2 - v_0^2 = 2gy}\)
鉛直上方投射 (鉛直上向きが正)
速度 \(\boldsymbol{v = v_0 - gt}\)
変位 \(\boldsymbol{y = v_0t - {\large{\frac{1}{2}}}gt^2}\)
\(t\) を含まない式 \(\boldsymbol{v^2 - v_0^2 = - 2gy}\)
鉛直上方投射 (鉛直下向きが正)
速度 \(\boldsymbol{v = - v_0 + gt}\)
変位 \(\boldsymbol{y = - v_0t + {\large{\frac{1}{2}}}gt^2}\)
\(t\) を含まない式 \(\boldsymbol{v^2 - v_0^2 = 2gy}\)
速度 \(\boldsymbol{v_x = v_0}\) \(\boldsymbol{v_y = gt}\)
位置 \(\boldsymbol{x = v_0t}\) \(\boldsymbol{y = {\large{\frac{1}{2}}}gt^2}\)
軌道の式 \(\boldsymbol{y = {\large{\frac{g}{2{v_0}^2}}}x^2}\)
速度 \(\boldsymbol{v_x = v_0\cosθ}\) \(\boldsymbol{v_y = v_0\sinθ - gt}\)
位置 \(\boldsymbol{x = v_0\cosθ⋅t}\) \(\boldsymbol{y = v_0\sinθ⋅t - {\large\frac{1}{2}}gt^2}\)
軌道の式 \(\boldsymbol{y = \tanθ⋅x - {\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}}x^2}\)
軌道の式はそのままを覚えるのは大変なので導出方法を覚えてください。また、斜方投射の式をこねくり回すと最高点の高さや時間、あるいは水平到達距離が求められます。これらも式を暗記するのではなく導出方法を覚えてください。
物体に外部から力がはたらかないとき、または、はたらいていてもその合力が 0 であるとき、静止している物体は静止し続け、運動している物体はそのまま等速度運動(等速直線運動)を続ける。
\(\boldsymbol{m\vec{a} = \vec{F}}\)
終端速度
\(ma = mg - kv\)
\(\boldsymbol{P = {\large{\frac{W}{t}}} = Fv}\)
\(\boldsymbol{K = {\large{\frac{1}{2}}}mv^2}\)
物体の運動エネルギーの変化は物体にされた仕事に等しい
\(\boldsymbol{{\large\frac{1}{2}}mv^2 - {\large\frac{1}{2}}{mv_0}^2 = W}\)
\(\boldsymbol{U = mgh}\)
\(\boldsymbol{U = {\large\frac{1}{2}}kx^2}\)
(保存力のみがはたらく場合)
運動エネルギー\(\boldsymbol{K}\) + 位置エネルギー\(\boldsymbol{U}\) = 力学的エネルギー\(\boldsymbol{E}\) = 一定
あらい水平面を進む物体のエネルギー
\({\large\frac{1}{2}}{mv_2}^2 - {\large\frac{1}{2}}{mv_1}^2 = - Fs = - μ'mgs\)
あらい斜面をすべり下りる物体のエネルギー
\(({\large\frac{1}{2}}{mv_2}^2 + mgy_2) - ({\large\frac{1}{2}}{mv_1}^2 + mgy_1) = - μ'mgs\cosθ\)
\(\boldsymbol{m\vec{v'} - m\vec{v} = \vec{F}Δt}\)
外力が無視できるとき、物体系の運動量の和は保存される
\(\boldsymbol{m_1\vec{v_1} + m_2\vec{v_2} = m_1\vec{v_1'} + m_2\vec{v_2'}}\)
\(\boldsymbol{e = - {\large\frac{v'}{v}} = {\large\frac{|v'|}{|v|}}}\)
- \(e = 1\) 弾性衝突(完全弾性衝突)
- \(0 ≦ e < 1\) 非弾性衝突
- \(e = 0\) 完全非弾性衝突
\(e = {\large\frac{v'}{v}} = {\large\frac{\sqrt{2gh'}}{\sqrt{2gh}}} = {\large\sqrt{\frac{h'}{h}}}\)
\(\boldsymbol{e = - {\large\frac{v_1{'}-v_2{'}}{v_1-v_2}}}\)
等速円運動の角速度
\(\boldsymbol{ω = {\large\frac{\theta}{t}}}\) あるいは \(\boldsymbol{θ = ωt}\)
\(\boldsymbol{v = rω}\)
\(\boldsymbol{T = {\large\frac{2\pi}{\omega}}}\)
\(\boldsymbol{n = {\large\frac{1}{T}} = {\large\frac{ω}{2\pi}}}\)
\(\boldsymbol{a = rω^2 = {\large\frac{v^2}{r}}}\)
\(\boldsymbol{F = mrω^2 = m{\large\frac{v^2}{r}}}\)
\(\boldsymbol{f = {\large\frac{1}{T}}}\)
\(\boldsymbol{ω = 2πf = {\large\frac{2\pi}{T}}}\)
\(\boldsymbol{x = A\sinωt}\)
\(\boldsymbol{v = Aω\cosωt}\)
\(\boldsymbol{T = 2π{\sqrt{\large\frac{m}{K}}}}\)
\(\boldsymbol{F = - kx}\)
\(\boldsymbol{T = 2π{\sqrt{\large\frac{m}{k}}}}\)
\(\boldsymbol{F = - kx}\)
\(\boldsymbol{T = 2π{\sqrt{\large\frac{m}{k}}}}\)
\(\boldsymbol{F = - {\large\frac{mg}{l}}x}\)
\(\boldsymbol{T = 2π{\sqrt{\large\frac{l}{g}}}}\)
\(\boldsymbol{E = {\large\frac{1}{2}}mω^2A^2}\)
\(\boldsymbol{ = {\large\frac{1}{2}}KA^2}\)
\(\boldsymbol{ = 2π^2mf^2A^2}\)
惑星は太陽を1つの焦点とする楕円軌道を描く。
惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である。
惑星の公転周期 \(\boldsymbol{T}\) の2乗は、楕円軌道の半長軸 \(\boldsymbol{a}\) の3乗に比例する。
\(\boldsymbol{F = G{\large\frac{Mm}{r^2}}}\)
\(mg = G{\large\frac{Mm}{R^2}}\) (地表付近)
\(\boldsymbol{U = - G{\large\frac{Mm}{r}}}\)
\(m{\large\frac{v^2}{R+h}} = G{\large\frac{Mm}{(R+h)^2}}\)
∴ \(v = \sqrt{\large{\frac{GM}{R+h}}}\)
第1宇宙速度(地表すれすれを飛び続けるための速度)
\(v = \sqrt{gR}\)
第2宇宙速度(脱出速度)
\(v = \sqrt{2gR}\)
電磁気
\(\boldsymbol{F = k{\large\frac{q_1q_2}{r^2}}}\)
\(\boldsymbol{\vec{E} = {\large\frac{\vec{F}}{q}}}\) \((\)\(\boldsymbol{\vec{F} = q\vec{E}}\)\()\)
\(\boldsymbol{E = k{\large\frac{q}{r^2}}}\)
\(\boldsymbol{\vec{E} = \vec{E_1} + \vec{E_2} + \vec{E_3} + …}\)
- 電気力線は正電荷から出て負電荷に入る。
- 電気力線は途切れたり急に始まったりしない。
- 電気力線は交わったり枝分かれしたりしない。
- 電場の強さが \(E\) [N/C] の場所に 1m2 当たり \(E\) 本の密度で電気力線を描くことにすると、電場の強さを電気力線の密度で表現できる。
総量 \(\boldsymbol{Q}\) [C] の電荷から出る電気力線の総数は \(\boldsymbol{4πkQ}\) 本
\(\boldsymbol{V = Ed}\)
電位差(電圧)
\(V = Ed\)
\(\boldsymbol{V = k{\large\frac{q}{r}}}\)
- 等電位面に沿って電荷を動かしても仕事は 0 。
- 等電位面と電気力線は常に直交する。
- 等電位面が密なところは電場が強い。
- 導体内部に電場は存在しない。
- 導体はどの部分も等電位である。
- 導体表面の電場の方向は導体表面に垂直である。
電気容量 \(\boldsymbol{C}\)
\(\boldsymbol{Q = CV = ({\large\frac{1}{4\pi k}\frac{S}{d}})V}\)
\(C = {\large\frac{1}{4\pi k}\frac{S}{d}} = (ε){\large\frac{S}{d}}\)
誘電率
\(ε = {\large\frac{1}{4\pi k}}\)
比誘電率
\(ε_r = {\large\frac{ε}{ε_0}}\)
\(C = ε_rC_0\)
\(Q = ε_rC_0V\)
\(\boldsymbol{U = {\large\frac{1}{2}}QV = {\large\frac{1}{2}}CV^2 = {\large\frac{Q^2}{2C}}}\)
コンデンサーの極板間引力
\(F = {\large\frac{Q^2}{2εS}} = {\large\frac{1}{2}}QE\)
コンデンサーの並列接続の合成容量
\(\boldsymbol{C = C_1 + C_2}\)
コンデンサーの直列接続の合成容量
\(\boldsymbol{{\large\frac{1}{C}} = {\large\frac{1}{C_1}} + {\large\frac{1}{C_2}}}\)
コンデンサーは
- 横方向に分割できる。
- 縦方向に分割できる。
- 順序を変えられる。
- 導体を挟んだ場合は、導体部分が圧縮されて無くなったとみなすことができる。
- 誘電体を挟んだ場合は、2つのコンデンサーを直列に接続したとみなすことができる。
\(\boldsymbol{V = RI}\)
抵抗率 \(\boldsymbol{ρ}\)
\(\boldsymbol{R = ρ⋅{\large\frac{l}{S}}}\)
抵抗率の温度係数 \(\boldsymbol{α}\)
\(\boldsymbol{ρ = ρ_0(1 + αt)}\)
\(W = qEd = qV\)
\(\boldsymbol{Q = IVt = I^2Rt = {\large\frac{\ V^2}{R}}t}\)
\(\boldsymbol{P = {\large\frac{W}{t}} = IV}\) (\(= I^2R = {\large\frac{\ V^2}{R}}\))
電力量
\(\boldsymbol{W = Pt = IVt}\) (\(= I^2Rt = {\large\frac{\ V^2}{R}}t\) ジュールの式と同じ)
電気回路の任意の分岐点について、そこに流れ込む電流の和は、そこから流れ出る電流の和に等しい。
電気回路の任意の一回りの閉じた経路について、電位差の和は 0 である。
\(\boldsymbol{R = R_1 + R_2}\)
\(\boldsymbol{{\large\frac{1}{R}} = {\large\frac{1}{R_1}} + {\large\frac{1}{R_2}}}\)
\(\boldsymbol{V = E - rI}\)
\(\boldsymbol{R_{\rm A} = {\large\frac{r_{\rm A}}{n-1}}}\)
\(\boldsymbol{R_{\small{\rm V}} = (n-1)r_{\small{\rm V}}}\)
\(\boldsymbol{{\large\frac{R_1}{R_2}} = {\large\frac{R_3}{R_4}}}\)
\(\boldsymbol{F = k_{\rm m}{\large\frac{m_1m_2}{r^2}}}\)
磁場 \(\vec{H}\)
\(\boldsymbol{\vec{F} = m\vec{H}}\)
- 磁力線はN極から出てS極に入る。
- 磁力線は途切れたり急に始まったりしない。
- 磁力線は交わったり枝分かれしたりしない。
- 磁場の強さが \(H\) [N/Wb] の場所に 1m2 当たり \(H\) 本の密度で磁力線を描くことにすると、磁場の強さを磁力線の密度で表現できる。
\(\boldsymbol{H = {\large\frac{I}{2\pi r}}}\)
磁場の向きは右ねじの法則に従う。
\(\boldsymbol{H = {\large\frac{I}{2r}}}\)
\(\boldsymbol{H = nI}\)
\(μ_{\rm r} = {\large\frac{μ}{μ_0}}\)
\(\boldsymbol{\vec{B} = μ\vec{H}}\)
\(\boldsymbol{Φ = BS}\)
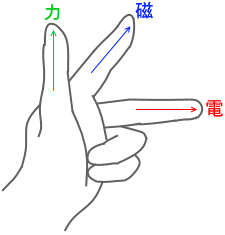
\(\boldsymbol{f = qvB\sinθ}\)
行っちゃーいやよ来ちゃいやよの法則
磁石を速く動かすほど、
磁石の磁力が強いほど、
コイルの巻き数が多いほど、
発生する誘導起電力が大きくなる。
\(\boldsymbol{V = - N{\large\frac{ΔΦ}{Δt}}}\)
\(\boldsymbol{V = vBl}\)
\(\boldsymbol{V = - L{\large\frac{ΔI}{Δt}}}\)
\(L = {\large\frac{μN^2S}{l}} = μn^2lS\)
\(\boldsymbol{U = {\large\frac{1}{2}}LI^2}\)
\(\boldsymbol{V_2 = - M{\large\frac{ΔI_1}{Δt}}}\)
\(M ∝ μn_1n_2S\)
\(\boldsymbol{{\large\frac{V_{1\rm{e}}}{V_{2\rm{e}}}} = {\large\frac{I_{2\rm{e}}}{I_{1\rm{e}}}} = \large{\frac{N_1}{N_2}}}\)
\(\boldsymbol{V_{\rm e} = {\large\frac{1}{\sqrt{2}\ }}V_0}\)
\(\boldsymbol{I_{\rm e} = {\large\frac{1}{\sqrt{2}\ }}I_0}\)
電圧 \(\boldsymbol{V = V_0\sinωt}\)
電流 \(\boldsymbol{I = {\large\frac{V_0}{ωL}}\sin\bigl(ωt - {\large\frac{π}{2}}\bigr)}\)
\(\boldsymbol{V_0 = ωLI_0}\)
\(\boldsymbol{X_{\rm L} = ωL}\)
電圧 \(\boldsymbol{V = V_0\sinωt}\)
電流 \(\boldsymbol{I = ωCV_0\sin\bigl(ωt + {\large\frac{π}{2}}\bigr)}\)
\(\boldsymbol{V_0 = {\large\frac{I_0}{ωC}}}\)
\(\boldsymbol{X_{\rm C} = {\large\frac{1}{ωC}}}\)
\(\boldsymbol{Z = \sqrt{R^{\small2}+(ωL-{\large\frac{1}{ωC}})^{\small2}}}\)
\(\boldsymbol{ω_0 = {\large\frac{1}{\sqrt{LC}}}}\)
\(\boldsymbol{f_0 = {\large\frac{1}{2π\sqrt{LC}}}}\)
\(\boldsymbol{f = {\large\frac{1}{2π\sqrt{LC}}}}\)
波動
\(\boldsymbol{f = {\large\frac{1}{T}}}\)
\(\boldsymbol{v = fλ}\)
波に関するグラフを読み取るときは、横軸が \(x\) であるか \(t\) であるか、注意が必要。
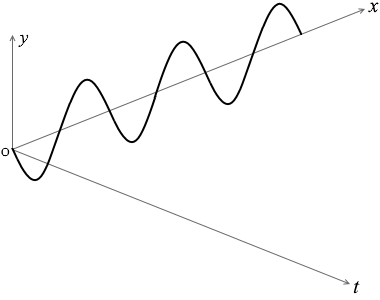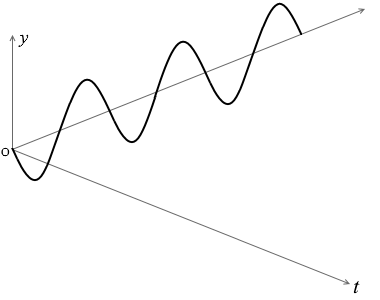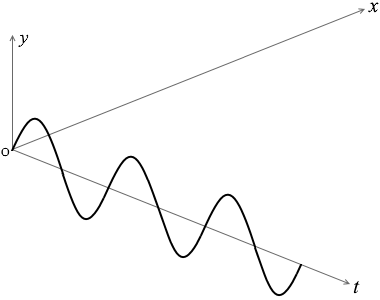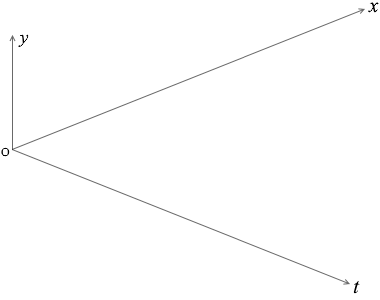
\(\boldsymbol{y = A\sin{\large\frac{2π}{T}}\big(t - {\large\frac{x}{v}}\big)}\)
\(\boldsymbol{= A\sin2π\big({\large\frac{t}{T}} - {\large\frac{x}{λ}}\big)}\)
強め合う条件 \(\boldsymbol{| l_1 - l_2 | = mλ}\)
弱め合う条件 \(\boldsymbol{| l_1 - l_2 | = (m+{\large\frac{1}{2}})λ}\)
\((m = 0,1,2,…)\)
\(\boldsymbol{{\Large\frac{\sin i}{\sin r}} = {\Large\frac{v_1}{v_2}} = {\large\frac{λ_1}{λ_2}} = n_{12} = 一定}\)
\(\boldsymbol{V = 331.5 + 0.6t}\) [m/s]
\(\boldsymbol{v_{\rm a} = {\large\frac{c}{\ n_{\rm a}}}}\)
\(\boldsymbol{n_{12} = {\large\frac{n_2}{n_1}}}\)
臨界角 \(\boldsymbol{i_0}\)
\(\boldsymbol{\sin i_0 = n_{12} = {\large\frac{n_2}{n_1}}}\)
屈折率の小さい媒質から大きい媒質へ進むときは臨界角は存在しない。全反射は起こらない。
\(\sin i_0 = {\large\frac{1}{n}} = {\large\frac{1}{1.333}} ≒ 0.750\) \(i_0 ≒ 48.6°\)
光の分散
<波長が長い>赤→橙→黄→緑→青→藍→紫<波長が短い>
\(\boldsymbol{λ_n = {\large\frac{2l}{n}}}\) \((n = 1,2,3,…)\)
\(\boldsymbol{f_n = {\large\frac{n}{2l}\sqrt{\frac{S}{\rho}}}}\) \((n = 1,2,3,…)\)
\(\boldsymbol{λ_{2n-1} = {\large\frac{4l}{\ 2n-1}}}\)
\(\boldsymbol{f_{2n-1} = {\large\frac{2n-1}{\ 4l}}V}\) \((n = 1,2,3,…)\)
\(\boldsymbol{λ_n = {\large\frac{2l}{\ n\ }}}\)
\(\boldsymbol{f_n = {\large\frac{n}{\ 2l}}V}\) \((n = 1,2,3,…)\)
\(\boldsymbol{f = {\large\frac{V-v_{\rm o}}{V-v_{\rm s}}}f_0}\)
\(f\):観測者が感知する振動数 \(V\):音速 \(f_0\):音源の振動数
\(v_{\rm o}\):観測者の速度 \(v_{\rm s}\):音源の速度 音源から観測者への向きを正とする
\(\boldsymbol{f = | f_1 - f_2 |}\)
明線の条件 \(\boldsymbol{{\large\frac{dx}{l}} = mλ}\)
暗線の条件 \(\boldsymbol{{\large\frac{dx}{l}} = (m+{\large\frac{1}{2}})λ}\)
\((m = 0,1,2,…)\)
明線の条件 \(\boldsymbol{d\sinθ = mλ}\)
暗線の条件 \(\boldsymbol{d\sinθ = (m + {\large\frac{1}{2}})λ}\)
\((m = 0,1,2,…)\)
明線の条件 \(\boldsymbol{d\sinθ = 0 , (m + {\large\frac{1}{2}})λ}\)
暗線の条件 \(\boldsymbol{d\sinθ = mλ}\)
\((m = 1,2,3,…)\)
明るくなる条件 \(\boldsymbol{2nd\cosθ = (m + {\large\frac{1}{2}})λ}\)
暗くなる条件 \(\boldsymbol{2nd\cosθ = mλ}\)
\((m = 0,1,2,…)\)
明るくなる条件 \(\boldsymbol{2x\tanθ = (m + {\large\frac{1}{2}})λ}\)
暗くなる条件 \(\boldsymbol{2x\tanθ = mλ}\)
\((m = 0,1,2,…)\)
明るいリングの条件 \(\boldsymbol{{\large\frac{\ r^2}{R\ }} = (m + {\large\frac{1}{2}})λ}\)
暗いリングの条件 \(\boldsymbol{{\large\frac{\ r^2}{R\ }} = mλ}\)
\((m = 0,1,2,…)\)
(凸レンズ)
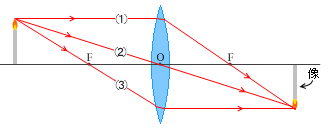 (1)光軸に平行な光線は、凸レンズを通った後、焦点を通る。
(1)光軸に平行な光線は、凸レンズを通った後、焦点を通る。
(2)凸レンズの中心を通る光線は、そのまま真っ直ぐ進む。
(3)焦点を通る光線は、凸レンズを通った後、光軸に平行に進む。
(凹レンズ)
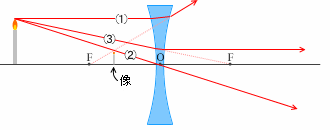 (1)光軸に平行な光線は、凹レンズを通った後、レンズ手前にある焦点から出たように進む。
(1)光軸に平行な光線は、凹レンズを通った後、レンズ手前にある焦点から出たように進む。
(2)凹レンズの中心を通る光線は、そのまま真っ直ぐ進む。
(3)レンズ後方の焦点に向かう光線は、凹レンズを通った後、光軸に平行に進む。
 レンズの一部が汚れていても像は映ります。若干うすくなりますが。
レンズの一部が汚れていても像は映ります。若干うすくなりますが。
\(\boldsymbol{{\large\frac{1}{a}} + {\large\frac{1}{b}} = \large{\frac{1}{f}}}\)
倍率 \(\boldsymbol{m = {\large\frac{|b|}{a}}}\)
物体とレンズとの距離 \(a\):常に正
レンズと像との距離 \(b\):レンズ後方は正、レンズ手前は負
焦点距離 \(f\):凸レンズは正、凹レンズは負
凹面鏡で反射する光
(1)
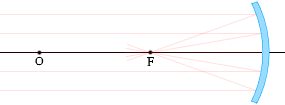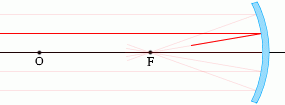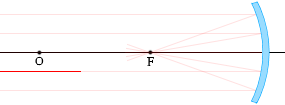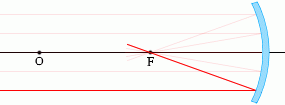 光軸に平行な光線は、反射し、焦点Fを通る。
光軸に平行な光線は、反射し、焦点Fを通る。
また、光の逆行により、焦点Fを通る光線は、反射し、光軸に平行に進む。
(2)
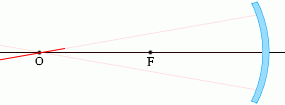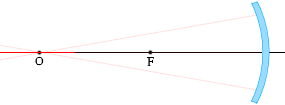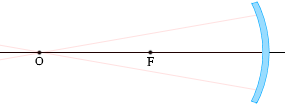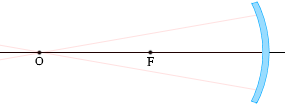 球の中心Oを通る光線は、反射し、再びOを通る。
球の中心Oを通る光線は、反射し、再びOを通る。
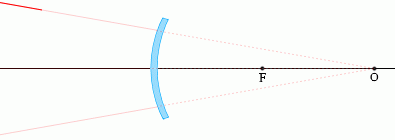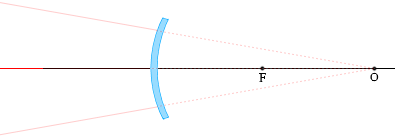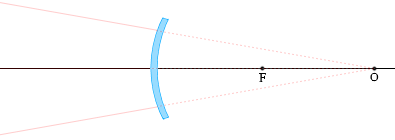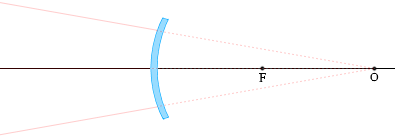
凸面鏡で反射する光
(1)
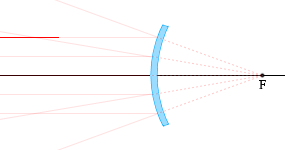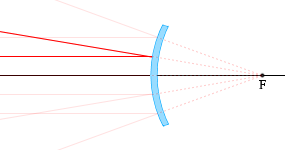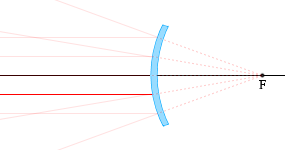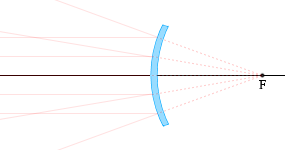 光軸に平行な光線は、反射し、焦点Fから出たように進む。
光軸に平行な光線は、反射し、焦点Fから出たように進む。
また、光の逆行により、焦点Fに向かう光線は、反射し、光軸に平行に進む。
(2)
 球の中心Oに向かう光線は、反射し、再び同じ経路を戻る。
球の中心Oに向かう光線は、反射し、再び同じ経路を戻る。
\(\boldsymbol{{\large\frac{1}{a}} + {\large\frac{1}{b}} = {\large\frac{1}{f}}}\)
倍率 \(\boldsymbol{m = {\large\frac{|b|}{a}}}\)
物体と球面鏡との距離 \(a\):常に正
球面鏡と像との距離 \(b\):球面鏡手前は正、球面鏡後方(裏側)は負
焦点距離 \(f\):球面鏡手前は正(凹面鏡)、球面鏡後方は負(凸面鏡)
熱力学
\(\boldsymbol{Q = CΔT}\)
\(\boldsymbol{Q = mcΔT}\)
高温物体が失った熱量 = 低温物体が得た熱量
熱の仕事当量 \(\boldsymbol{J = 4.19}\) J/cal
\(\boldsymbol{W = JQ}\)
質量が一定のとき、気体の体積 \(\boldsymbol{V}\) は、圧力 \(\boldsymbol{p}\) に反比例し、絶対温度 \(\boldsymbol{T}\) に比例する
\(\boldsymbol{{\large\frac{pV}{T}} = k}\)(一定)
あるいは
\(\boldsymbol{{\large\frac{p_1V_1}{T_1}} = {\large\frac{p_2V_2}{T_2}}}\)
\(\boldsymbol{pV = nRT}\)
\(\boldsymbol{p = {\large\frac{Nm\overline{{v}^2}}{3V}}}\)
\(\boldsymbol{{\large\frac{1}{2}}m\overline{{v}^2} = {\large\frac{3}{2}}kT}\)
\(\boldsymbol{\sqrt{\overline{{v}^2}} = \sqrt{{\large\frac{3RT}{M×10^{-3}}}}}\)
\(\boldsymbol{U = {\large\frac{3}{2}}nRT}\)
熱力学第1法則(外力の仕事を\(W\)とする)
\(\boldsymbol{ΔU = Q + W}\)
熱力学第1法則(気体の仕事を\(W\)とする)
\(\boldsymbol{Q = ΔU + W}\)
仕事と圧力と体積変化の関係
\(\boldsymbol{W = pΔV}\)
外部から加えた熱量を \(Q\) 、外部からの仕事を \(W\) とした場合
定積変化
\(\boldsymbol{ΔU = Q}\) \(\boldsymbol{{\large\frac{p\color{#bbb}{V}}{T}} =}\)(一定)
定圧変化
\(\boldsymbol{ΔU = Q - pΔV}\) \(\boldsymbol{{\large\frac{\color{#bbb}{p}V}{T}} =}\)(一定)
等温変化
\(\boldsymbol{0 = Q + W}\) \(\boldsymbol{{\large\frac{pV}{\color{#bbb}{T}}} =}\)(一定)
断熱変化
\(\boldsymbol{ΔU = W}\) \(\boldsymbol{{\large\frac{pV}{T}} =}\)(一定)
\(\boldsymbol{Q = nCΔT}\)
\(\boldsymbol{C_{\rm V} = {\large\frac{3}{2}}R = {\large\frac{3}{2}}⋅8.31 ≒ 12.5}\) J/(mol⋅K)
\(\boldsymbol{C_{\rm p} = {\large\frac{5}{2}}R = {\large\frac{5}{2}}⋅8.31 ≒ 20.8}\) J/(mol⋅K)
\(\boldsymbol{C_{\rm p} = C_{\rm V} + R}\)
\(\boldsymbol{γ = {\large\frac{C_{\rm p}}{C_{\rm V}}}}\)
エネルギーの変換において、それに関わったエネルギーの総量は一定である。
\(\boldsymbol{e = {\large\frac{W}{\ Q_1}} = {\large\frac{Q_1-Q_2}{Q_1}}}\)
原子
\(\boldsymbol{E = hν = {\large\frac{hc}{λ}}}\)
\(\boldsymbol{hν = {\large\frac{1}{2}}mv^2 + W}\)
または
\(\boldsymbol{K_{\rm{\small M}} = hν - W}\)
X線の最短波長
\(λ_0 = {\large\frac{hc}{eV}}\)
\(\boldsymbol{2d\sinθ = nλ}\) \((n =1,2,3,…)\)
\(\boldsymbol{p = {\large\frac{hν}{c}} = {\large\frac{h}{λ}}}\)
\(\boldsymbol{⊿λ = {\large\frac{h}{mc}}(1 - \cosφ)}\)
物質波(ド・ブロイ波)
\(\boldsymbol{λ = {\large\frac{h}{p}} = {\large{\frac{h}{mv}}}}\)
水素原子のスペクトル(リュードベリの式)
\(\boldsymbol{{\large\frac{1}{λ}} = R\Big({\large\frac{1}{n'^2}} - {\large\frac{1}{n^2}}\Big)}\)
\((n' = 1,2,3,…)\)
\((n = n'+1,n'+2,n'+3,…)\)
\(\boldsymbol{mvr = n{\large\frac{h}{2π}}}\) \((n = 1,2,3,…)\)
\(\boldsymbol{E_n - E_{n'} = hν}\)
\(\boldsymbol{r = {\large\frac{h^2}{4π^2k_0me^2}}⋅n^2}\) \((n = 1,2,3,…)\)
\(\boldsymbol{E_n = - {\large\frac{2π^2{k_0}^2me^4}{h^2}}⋅{\large\frac{1}{n^2}}}\) \((n = 1,2,3,…)\)
α崩壊:α線(\(\ce{^4_2He}\)の原子核)を放出する放射性崩壊。質量数が4、原子番号が2、減少する。
β崩壊:β線(\(e^-\))を放出する放射性崩壊。質量数は変わらず、原子番号が1増加する。
γ崩壊:γ線(電磁波)を放出する放射性崩壊。質量数も原子番号も変わらない。
| 実体 | 電荷 | 電離作用 | 透過力 | 電場中の方向 | 磁場中の方向 | |
|---|---|---|---|---|---|---|
| α線 | 高速の\(\ce{^4_2He}\)原子核 | \(+2e\) | 大 | 小 | 負極へ | 電流と同じ |
| β線 | 高速の電子 | \(-e\) | 中 | 中 | 正極へ | 電流と逆 |
| γ線 | 短波長の電磁波 | 0 | 小 | 大 | 直進 | 直進 |
半減期 \(\boldsymbol{T}\)
\(\boldsymbol{N = N_0{\large(\frac{1}{2})^\frac{t}{T}}}\)
質量欠損 \(\boldsymbol{ΔM}\)
\(\boldsymbol{ΔM = Zm_{\rm p} + (A-Z)m_{\rm n} - M}\)
\(\boldsymbol{E = mc^2}\)